NeuroMLR: Robust & Reliable Route Recommendation on Road Networks

NeurIPS 2021 Poster

• Paper
• Source code
• Open review & Appendix
• 相关survey

0. Summary

0.1 本文解决的问题

1. 大部分路径推测算法无法到达destination
2. 现存的方法都是Transductive Learning (转导学习)，所以在inference时无法处理没见过的路线。

▶

Inductive/Transductive Learning

Inductive Learning (归纳学习)
归纳学习是一种更常见的学习方式，它基于从特定的训练样本中学习并推广到未见过的新样本的模式。

Transductive Learning (转导学习)
转导学习与归纳学习相对，不是试图建立一个普遍的模型，而是专注于从已知的特定训练数据直接推断测试集中样本的标签或属性。转导学习的目的是对特定的未标记数据集进行预测，而不是创建一个通用的模型。

0.2 本文的主要贡献

1. 将路径推荐问题解耦为 路径搜索（route search） 和现有路径到达一个节点后的 转移概率预测（transition probabilities prediction） 两部分。
2. 转移概率预测部分使用Inductive Learning，提出用NeuroMLR方法，即使用Lipschitz embeddings 和 GCN 对转移概率进行建模，在未见过和训练期间很少见到的节点上也有很好的泛化。

1. Background

路径推荐任务：基于历史路径数据，给定source node 和 destination node，预测 most likely route。

1.1 Baselines

• DEEPST: 使用VAE
• CSSRNN：使用RNN
• shortest path (SP)
• quickest path (QP)

1.2 Problem Formulation

路网(Road Network) 用有向图 $\mathcal{G}=(\mathcal{V},\mathcal{E},\delta,\tau_t)$ 表示，其中

• $\delta:\mathcal{E}\to\mathbb{R}$ 表示边的长度
• $\tau_{t}:\mathcal{E}\to\mathbb{R}$ 是经过边的平均时间

路径(Route) 从source到destination：

• 用节点表示：$\mathcal{R}(s,d)=\{v_{1},\cdots,v_{k}\}$
• 用边表示：$\mathcal{R}(s,d)=\{e_{1},\cdots,e_{k-1}\}$

Historical trajectories 一个保存了GPS历史轨迹的数据集 $D$ ，每个数据由<latitude, longitude, time>表示

Query 一个路径查询，由 $q = <s,d,t>$表示，代表出发点、终点、出发时间。

Most Likely Route：

$$\mathcal{R}^*(s,d)=\arg\max_{\forall\mathcal{R}(s,d)\in\mathcal{G}}Pr_D(\mathcal{R}(s,d)\mid q)$$

把上面的概率用条件概率展开：

$$Pr_D(\mathcal{R}\mid q)=\prod_{i=1}^{|\mathcal{R}|}Pr_D(\mathcal{R}.e_i\mid\mathcal{R}.e_0\to\mathcal{R}.e_{i-1},s,d,t)$$

表示已知从第0个边到第$i-1$的边已知，剩余路径的概率。

使用Markov假设，即下一条边的选择仅取决于当前节点：

$$Pr_D(\mathcal{R}\mid q)=\prod_{i=1}^{|\mathcal{R}|}Pr_D(\mathcal{R}.e_i\mid v_i,d,t)$$

因此原问题转化为

$$\mathcal{R}^*(s,d)=\arg\max_{\forall\mathcal{R}\in\mathcal{G}}\prod_{i=1}^{|\mathcal{R}|}Pr_D(\mathcal{R}.e_i\mid v_i,d,t)\quad=\arg\min_{\forall\mathcal{R}\in\mathcal{G}}\sum_{i=1}^{|\mathcal{R}|}-\log(Pr_D(\mathcal{R}.e_i\mid v_i,d,t))$$

至此，问题被解耦为：

1. 根据历史轨迹数据集D对概率建模：$Pr_D$
2. 根据模型搜索最可能路径 $\mathcal{R}^*$

2. Method

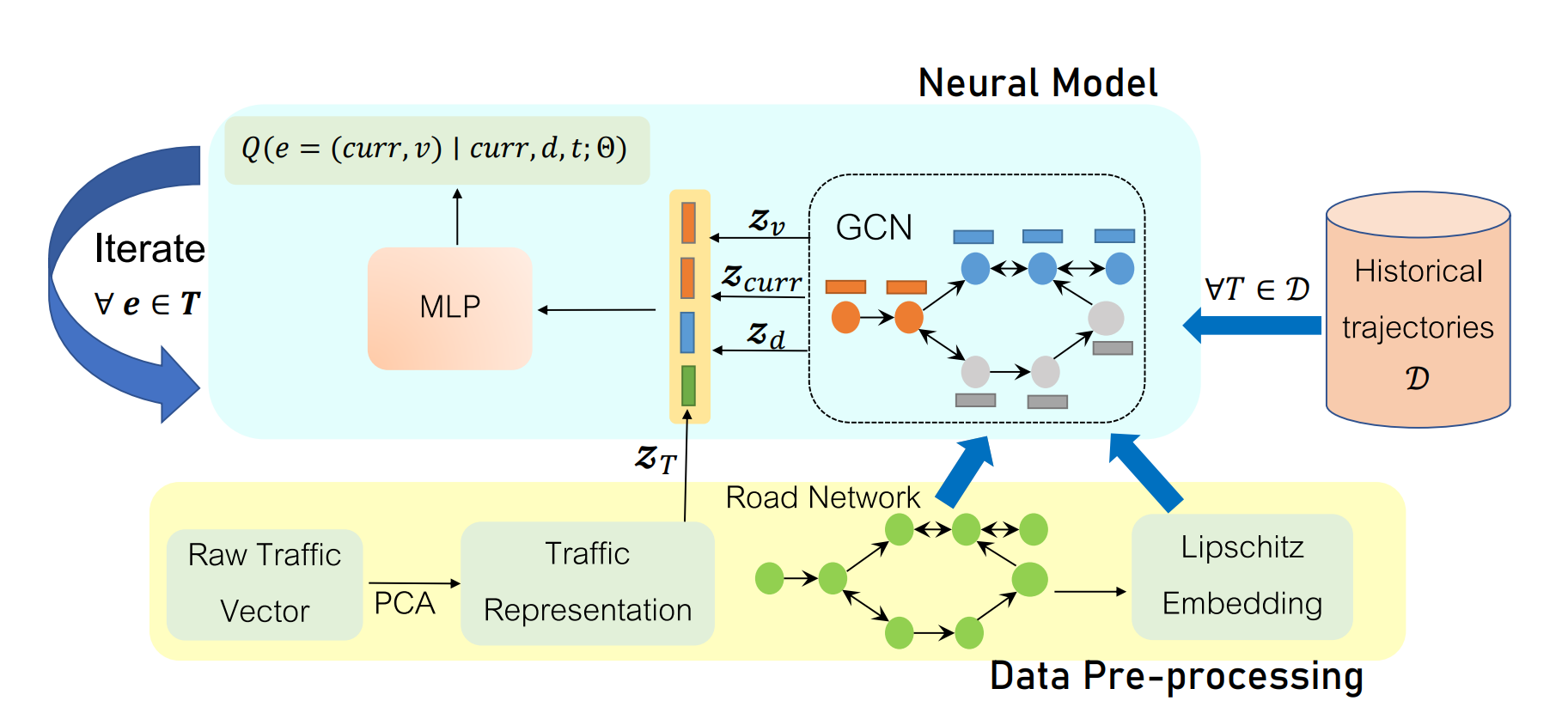
2.1 概率建模

本文使用MLP作为代理函数（surrogate function）近似真实分布：

$\text{MLP}(v, curr, d, t;\Theta) \approx P(e=(curr,v)\mid curr, d, t)$

其中$\Theta$是从数据集$D$中学习到的参数。

2.2 Node representation

假设: 在嵌入空间中，通往共同目的地的距离相似的节点距离应当接近。

论文原文中说的是

在嵌入空间中，通往共同目的地的路径相似的节点距离应当接近。

但论文的实现是按照距离相似设计的distance函数。

因此按照以下方法对node定义嵌入度量空间$(\mathbb{R}^p,d)$：

1. 随机选择 $p$ 个点作为 anchor $\mathcal A = \{a_1, ... , a_p\}$
2. 在 $\mathcal{V}$ 上定义距离函数 $d_\mathcal{V}(u,v) = \frac{1}{2}(sp(u,v)+sp(v,u))$，其中$sp$是 spatial shortest path distance
3. 每个 $\mathcal{V}$ 中的点 $u$ 在 $\mathbb{R}^p$ 的嵌入表示就是 $[d_\mathcal{V}(u,a)]_{a\in \mathcal A}$
4. $d$ 可以用任意 $l_p$

2.2.1 Lipschitz embedding

Lipschitz embedding即对两个度量空间(metric space): $(\mathcal{O},d)$ 和 $(\mathcal{O}',d')$，一个 embedding function $f:\mathcal{O}\to\mathcal{O}^{\prime}$ 是Lipschitz的。

Bourgain’s Theorem保证了有限维的情况下，Lipschitz embedding的存在：

$$\forall (\mathbb{R}^p,d), \exist (\mathbb{R}^q,d'), \exist f:(\mathbb{R}^p,d)\to(\mathbb{R}^q,d') \text{ lipschitz}$$

where

• $q=O(\log^2n)$
• distortion (即Lipschitz常数) = $O(log|\mathcal{V}|)$

论文的具体实现方法在[13]。

2.2.2 GCN

训练前，所有节点的信息即为 Lipschitz embedding后的嵌入。

训练时，没有见过的节点的嵌入不会被更新。

为了解决这一问题，引入L层GCN。对于任何一个不在训练集的节点，只要它的L-hop节点在训练集里，它的嵌入也可以被更新了。

Embedding有没有被更新？还是只训练了GCN的weight？需要看代码进一步确认。

2.3 Traffic representation

交通堵塞情况可以用一个矩阵表示，维度分别是道路（图上的边）和时间。

• 道路维度：道路使用的频率服从幂律分布，因此只选择最常用的5%的道路
• 时间维度：没有按照以往的工作，假设每天流量一样，把每天分成多个短时间。实际咋做的也没说。

因为相接道路的堵塞情况相近，使用PCA降维。

2.4 整体训练过程

1. 选择$p$个anchor，构造节点嵌入空间$\mathbb{R}^p$.
2. 按照[13]的方法，构造lipschitz映射，降维嵌入空间至$\mathbb{R}^q$.
3. 用GCN传播相邻节点信息
4. 把GCN学习到的，在curr, v, d三个节点（当前、下一跳、终点）上的表示concatenate。
5. 把t时刻的Traffic representation也concatenate进去。
6. 对每一个v，输入进MLP，预测下一个节点的概率。（MLP输出标量）
7. 对所有v，计算输出softmax得到概率
8. 用cross-entropy作为loss学习

作者试了把MLP的输入加了attention，结论是没用 （Appendix N）

2.5 Inference - Route search

概率建模好之后要规划路径。

2.5.1 Optimal Search

Dijkstra。图的边的权重可以用$-log P$表示。（合理，路径的长度就是概率的乘积）。

2.5.2 Greedy Search

深度优先。每次选择概率最大的边。为了避免走错路，每次迭代时计算当前节点到终点的地理距离x和已走过路径到终点的最短距离y。如果 x >> y 则回溯。因为常理上汽车应该离终点的地理距离越来越近。

3. Experiments

3.1 Datasets

五个城市：Chengdu(CHG) Porto(PT) Harbin(HRB) Beijing(BJG) CityIndia(CTI)

均来自不同数据源。处理后的数据集在Github上。

使用map-matching方法把GPS数据对齐到OpenStreetMap的路网上。

3.2 Metrics

Precision、Recall、Reachability、Reachability Distance.

4. Results

4.1 Comparative Study

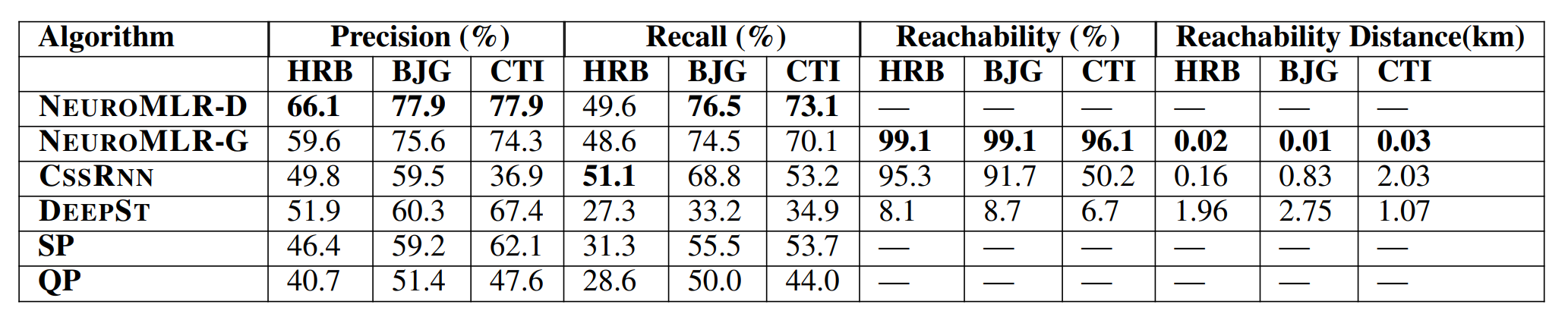
最优。NEUROMLR-G速度快于CSSRNN。

4.2 Inductive Learning

• 减少训练数据后，NeuroMLR优于CSSRNN
• 在起终点是不常见的顶点时，NeuroMLR优于CSSRNN

4.3 Ablation study

结论：GCN and Lipschitz Embeddings有用。Traffic没用，和其他论文一致。

5. 锐评

• 很咖喱：

  1. 论文写的挺烂。有typo，notation混用，实验细节完全不说，Appendix也没写。
  2. 代码0注释。太天才啦。

• MLP每次只能算一个节点的概率，效率太低了。

• MLP感觉是强行把每个节点的概率在参数里记录下来了，太暴力了。应当用一些包含inductive bias的方法。

• 没有找到之后follow的work

• 很简单很intuitive的模型